纵向数据广泛存在于经济学、流行病学、医学和社会学等领域。纵向数据的观察过程包括个体层面和时间层面,它的一个重要特点是,每个个体在不同时间点上的观测值是相依的,而不是独立的。由于纵向数据的广泛存在性和结构特殊性,已经有很多文献研究纵向数据,包括纵向数据分位数回归方面的研究。
近日,统计交叉科学研究院和统计学院马慧娟副教授与山东大学赵玮副研究员、美国埃默里大学John Hanfelt教授和Limin Peng教授合作,在纵向数据分位数回归研究方面取得一项重大研究成果,该成果发表在统计学顶级期刊Journal of the American Statistical Association上。


传统的纵向数据分位数回归模型研究观测到的纵向数据与协变量在给定时间 t 时的相关关系,这种边际模型方法类似于广义估计方程方法。有一些文献处理中途离开或者带有删失的纵向响应变量。还有一些文献对观测到的纵向数据分位数在给定协变量和个体固定(或随机)效应下进行建模。这些都是对观测到的纵向数据在给定时间点(即横截面数据)的分位数进行建模。
在许多实际情况中,研究人员对纵向数据个体层面的轨迹变化更感兴趣,但是已有的对纵向数据横截面的建模方式并不足够,因为横截面分位数随着时间的变化模式不能够反应个体层面轨迹的变化模式。例如,老年人的认知衰退速率存在显著差异,这是与衰老相关的脑部疾病的重要指标。理解认知衰退速率的异质性,有助于揭示与衰老相关的脑部疾病差异。这类轨迹特征(即潜在个体轨迹特征)通常无法直接观测,因为观测数据往往是潜在连续轨迹在离散时间点(如定期随访)的表现,且混杂着测量误差。
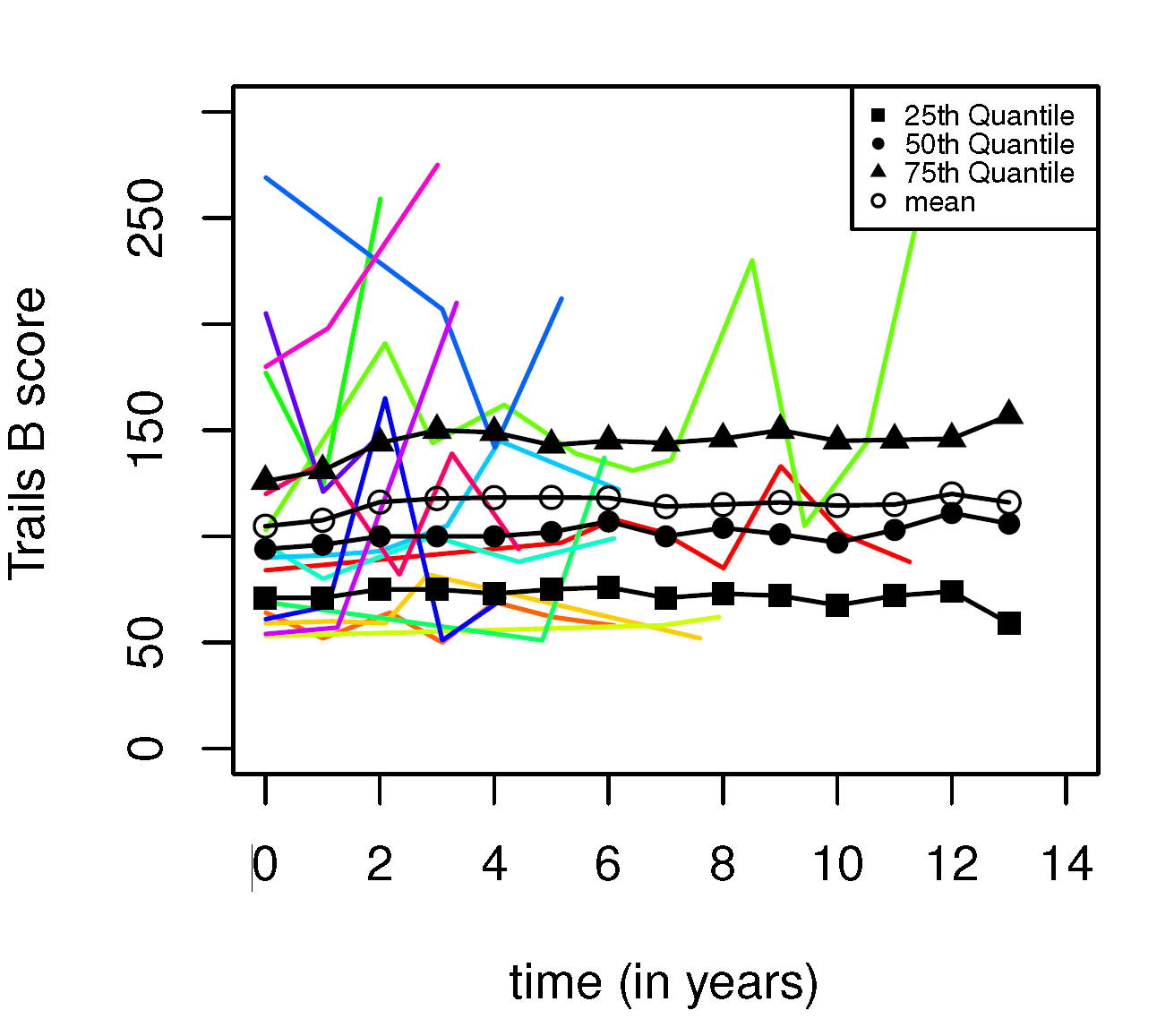

本研究提出纵向数据分位数回归模型以探究潜在个体轨迹特征的异质性模式。这是首次基于多层模型对潜在个体轨迹特征进行研究。该方法妥善解决了现有多层建模方法的局限性,在实际应用中可提供新颖分析,助力探究如阿尔茨海默病等痴呆疾病进展中的差异(以认知衰退为表征)。
具体而言,在第一层模型中,采用带个体随机参数的伪 B 样条(Pseudo B-Spline)模型,以灵活形式描述个体轨迹,同时允许非正态分布的随机误差。在第一层模型基础上定义目标潜在个体轨迹特征后,进一步利用分位数回归刻画观测协变量对潜在个体轨迹的影响。作为传统线性回归的重要扩展,分位数回归允许协变量效应在潜在个体轨迹分布的不同区间存在异质性,同时避免第二层模型中对潜在个体轨迹的参数分布假设(这是标准纵向多层模型的典型要求)。
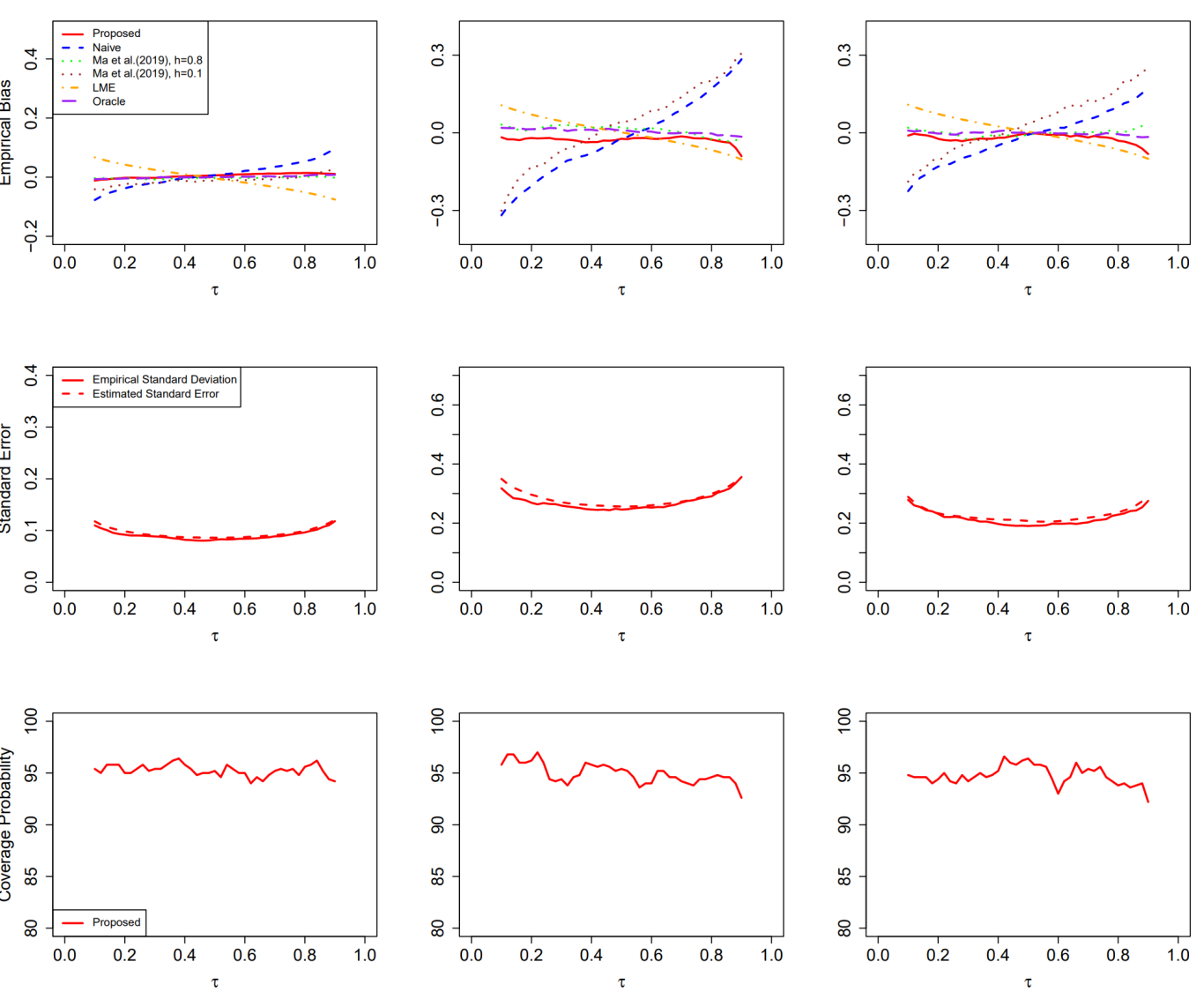
本研究基于条件得分原则提出了新颖的估计方法,并开发了高效的算法实现方案。大量模拟研究证实,该方法所得估计量具有理想的渐近性质和良好的有限样本性能。本研究将新提出的方法应用于一项对轻度认知障碍患者认知衰退的研究,为揭示轻度认知障碍患者认知衰退的复杂异质性表现提供了有价值的洞见。
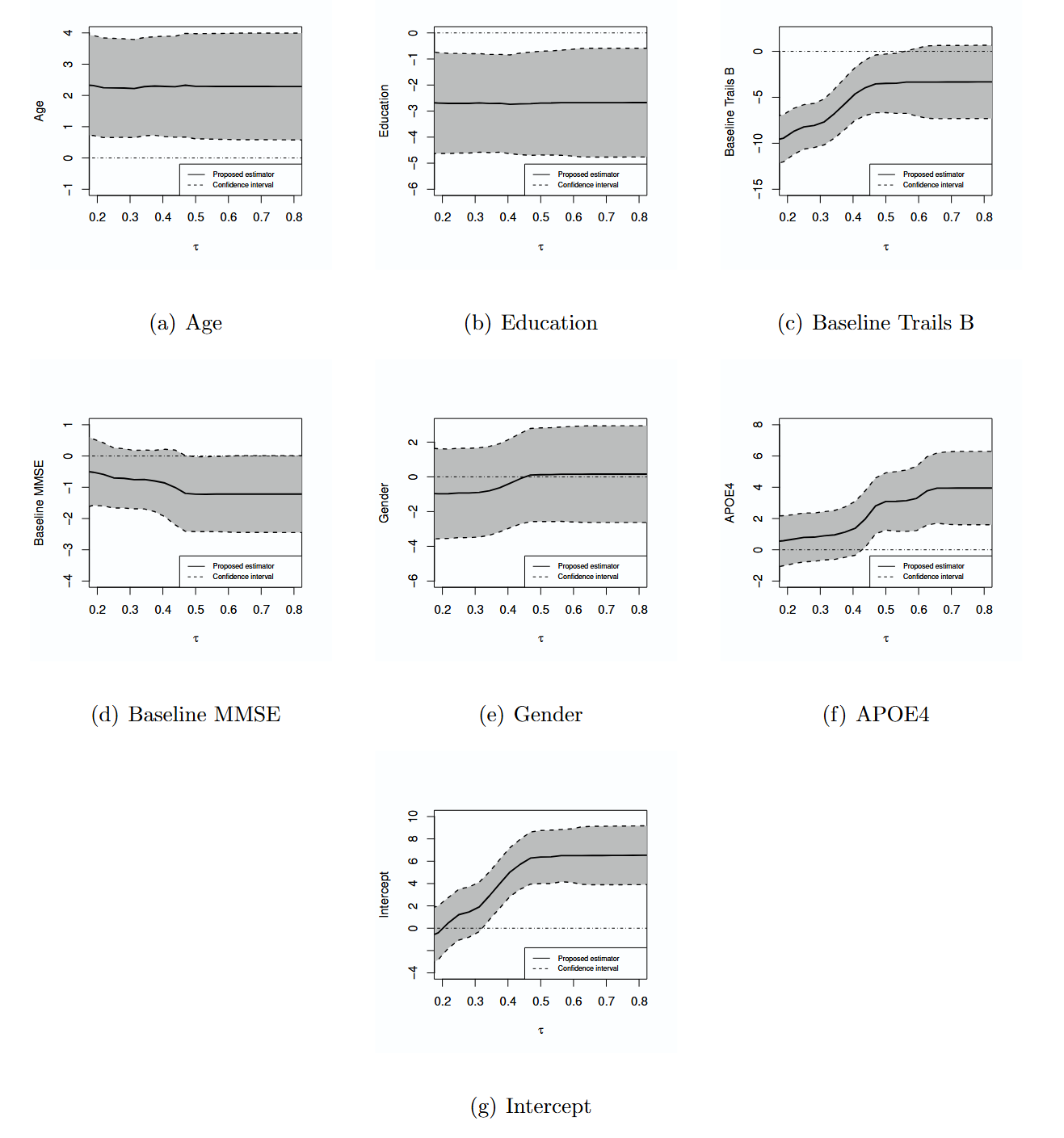
本次研究成果的取得,离不开跨机构、跨学科的国际科研合作。马慧娟2015年至2018年埃默里大学读博士后期间,充分利用埃默里大学的优质资源,在Limin Peng教授的指导下,已开展本课题方面的相关研究,经过近十年的攻关,终于取得新的突破。相关工作得到了国家自然科学基金委、上海市与华东师大的资助。
华东师范大学统计交叉科学研究院一直致力于拓展国际交流合作,鼓励教师与国际知名学者开展联合研究,注重培养教师的国际视野。研究院还通过举办国际学术论坛、邀请海内外知名学者讲学等方式,持续拓展国际合作网络。未来,研究院将进一步深化与全球知名高校和研究机构的合作,聚焦统计与数据科学前沿问题,共同推动统计交叉科学领域的发展与创新。



